7.3 Living longer than you expect
We’ve heard this so many times - “life expectancy is increasing”. “Singapore has one of the highest life expectancies in the world.” But what does the term “life expectancy” mean?
Figure 7.6: Screenshot of online article on life expectancy. Retrieved September 17, 2019.
A typical article (such as this one written by a physician) will use estimates of life expectancy to say, for instance, “Singaporean residents can expect to live up to 83.2 years67”. This reading of life expectancy is quite common.
The obvious question here is - Who can expect to live up to 83.2 years? My grandma? Me? My child? Do all Singaporeans now expect to live to the same age68?
The figure most often cited in the media is life expectancy at birth. A more precise way to interpret the life expectancy in 2017 is “Singaporean residents who are born in 2017 can expect to live to 83.2”. This other news article in the Straits Times rightly refers to the life expectancy estimate as “expected lifespan at birth”.
But this still does not fully capture how life expectancy is calculated. To do this, we need to go back to our understanding of age, period, and cohort measures. Life expectancy, as it is reported yearly, is a period measure.
Without going into full detail (interested readers can refer to resources such as this), I will explain briefly how this is calculated. A typical life table from the Department of Statistics (taken from this report) looks like Figure 7.7 (it shows just the top part, the entire table is a few pages long).
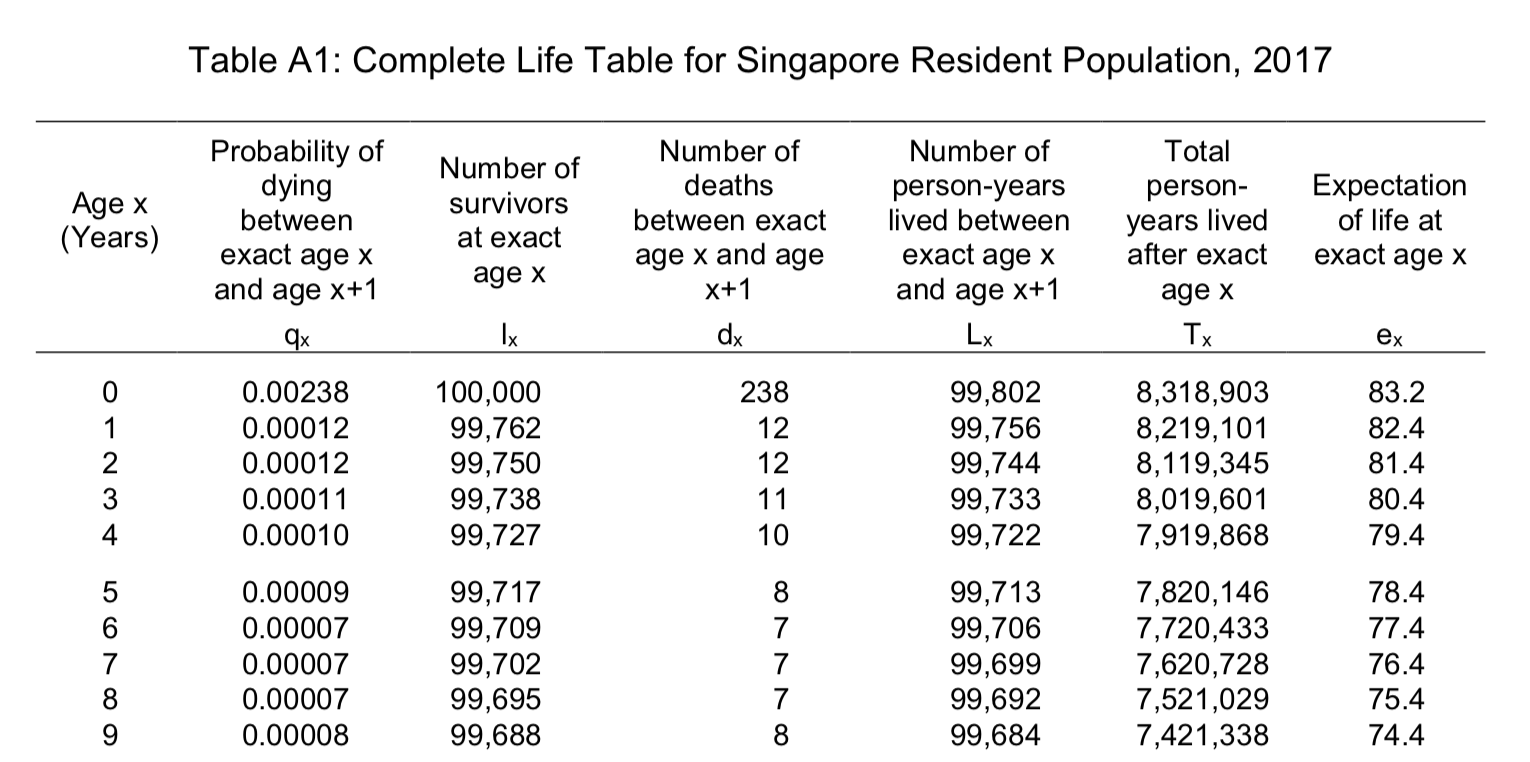
Figure 7.7: Screenshot of Complete Life Table from the Department of Statistics. Retrieved September 17, 2019.
Age-specific mortality rates (not pictured, but often referred to as ) for a specific year are obtained from the national mortality database and turned into69 the probability of dying in a specific age-interval (, pictured).
You start with a hypothetical base population, usually 100,000, and you put them through the mortality rates of each age until there are no more survivors (). In other words, the probability of dying at an age-interval becomes certain () at some point (usually 100+) since no one is immortal.
From there, you calculate a number of other things (e.g., , , , using simple math formulas). These numbers then help you derive the life expectancy (basically, ).
You may not yet fully understand what is happening here, but just note one key thing - the key quantities here that affect everything else in the whole process are the age-specific mortality rates (). And these age-specific mortality rates used in calculating life expectancy are a period measure, which capture what is happening that particular year.
To understand what this means for how we interpret life expectancy, we return to our previous interpretation - that “Singaporean residents who are born in 2017 can expect to live to 83.2”.
Let’s now make it more precise and say that “Singaporean residents who are born in 2017 and who are exposed to mortality rates of 2017 throughout their lives can expect to live to 83.2”.
This sounds highly awkward, I know. You would have to imagine some kind of time machine allowing you to stay stuck in 2017, continuing to experience its mortality rates even as you grow older. But it is in fact how the measure is calculated. Life expectancy, as often cited in the media, is a period measure that is constructed by stitching together the experiences of multiple cohorts (often called a synthetic cohort).
A more intuitive measure of life expectancy is called cohort life expectancy. Cohort life expectancy follows every person who was born in a certain year (e.g., 1965), and is calculated using the observed/projected rates of all persons in that cohort. With cohort life expectancy, we can truly say that “Singaporean residents born in year XXXX live XX.X years on average”. So why don’t we do this? The answer is simple - to obtain observed rates, we need to observe these deaths for each cohort! We would therefore need to wait for all (or most70) of each cohort to pass away before we can calculate such numbers.
Period life expectancy is therefore practical to use as a measure of how well our health system is doing from year to year, but we must acknowledge its limitations. In order to examine how volatile period rates of life expectancy can be, we can simply look at older rates of life expectancy.
But first, a small excursus - if you look back at Figure 7.7, one thing you will realize is that there are life expectancy estimates for each age. Therefore, life expectancy at age 40 is not the same as life expectancy at birth, and they do not usually add up (i.e., Life expectancy at 40 Life expectancy at birth - 40). Knowing this, we can now do a little thought experiment with life expectancy estimates.
Let us now look at life expectancy at birth in the year 1965. Using the Department of Statistics Table Builder (go here) to retrieve the data, it seems life expectancy at birth for Singapore residents back in 1965 was 64.5. Using the common way of interpreting these data, we might say, “we can expect those born in 1965 to live up to 64.5 years old.”
Fast forward to 2017, and those born in 1965 are now 52 years old. If those numbers in 1965 are correct, it follows that we might expect life expectancy at 52 to be years. Let’s go back to the Complete Life Tables we were looking at before to see how long more those born in 1965 can expect to live (Figure 7.8).
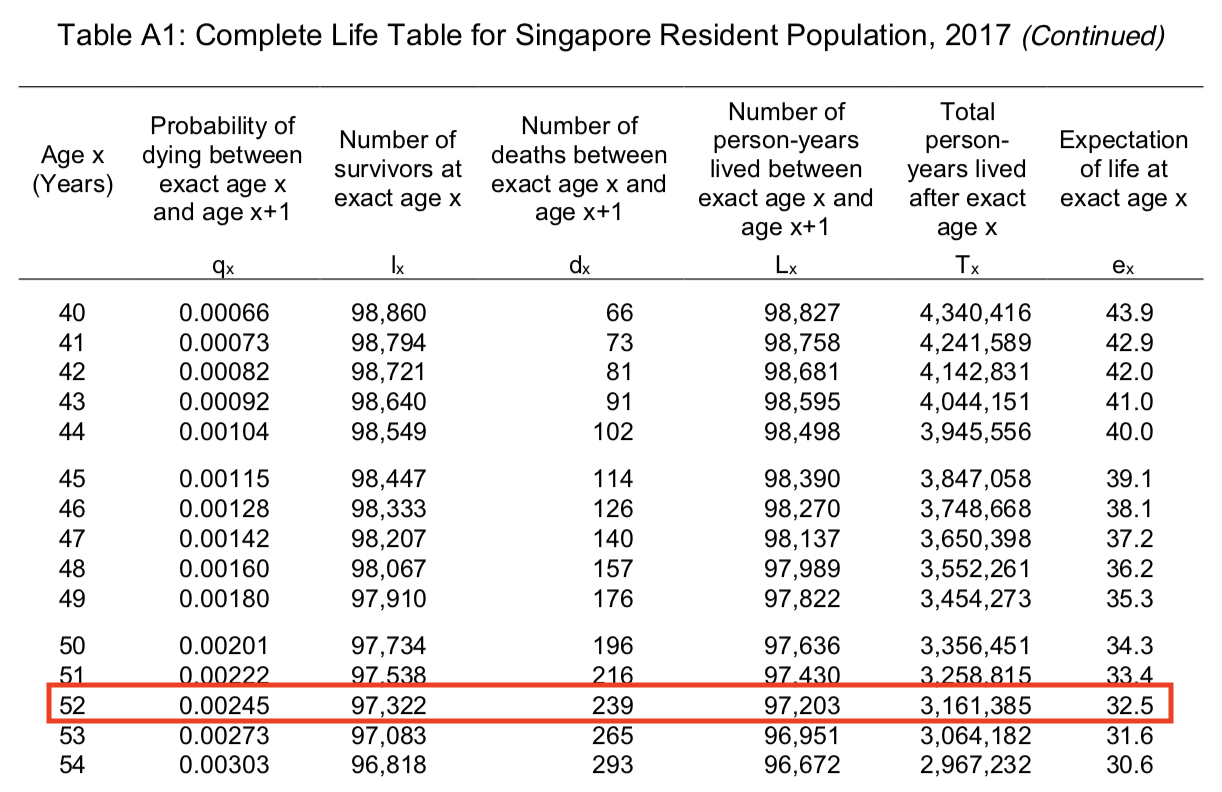
Figure 7.8: Screenshot of Complete Life Table from the Department of Statistics. Retrieved September 17, 2019.
Wait. We see now that those who aged 52 in 2017 can in fact expect to live 32.5 more years. That means they are expected to live up to years old! That seems way different from the 64.5 years projected by mortality statistics in 1965. Why is this so? This is because period life expectancy does not account for future improvements in mortality driven by better healthcare, hygiene, health behaviors etc. Period life expectancy is therefore often an underestimate of the true cohort life expectancy71. The discrepancy we see between the 1965 life table and the 2017 life table is likely due to great improvements in mortality rates since independence.
Having studied how life expectancy ‘works’, let us conclude by evaluating this paragraph from an article on the Dollars and Sense website, aimed at helping Singaporeans plan their retirement:
The next step of the retirement planning equation is to understand how long we can expect to spend in retirement. The longer we spend in retirement, the more we need to sustain ourselves.
How Long Do We Spend In Retirement? The simplest way to derive this figure is to use the average life expectancy of Singaporeans – which stands at 83.1 years today. This figure is only going to go up as the latest report from the World Health Organisation (WHO) revealed that people here can expect to live up to 85.4 years by 2040.
What this tells us is that if we retire at the moment we are able to receive our CPF LIFE payouts – at 65 – and live to the average life expectancy in Singapore – to 83.1 – we will have close to 18 years of retirement.
What are the misinterpretations of life expectancy present here? First, the writer talks about average life expectancy as if it applies to everyone. As we discussed, however, the number he uses likely reflects the life expectancy at birth. Is he speaking to newborns and asking them to plan for retirement? A better approach would be to go to the Complete Life Tables published by the Department of Statistics and refer to life expectancy at 50 (or some other reference age that his target audience can identify with). Second, he is correct that life expectancy will probably continue to rise, but the 18 years (obtained supposedly using ) is likely an underestimate of how long “retirement” will be (apart from the error already made in the first point). Plan harder, people.
The figure for the year 2017.↩︎
If this is true, then if life expectancy increases faster than one year annually, does this mean we can all expect to be immortal? You can see how ludicrous this sounds.↩︎
Some assumptions need to be made here about a quantity called , which captures when most deaths in a certain age-interval happen within the time period, but usually this calculation is straightforward.↩︎
Using a mixture of observed and projected rates is possible.↩︎
Unless mortality rates spike due to events such as wars, famines etc.↩︎