6.3 Non-probability sample, now what

Probability samples are hard to come by, and while in theory they are the “gold standard”43, there are a number of drawbacks when trying to implement them:

  1. Poor response rates. Not all respondents in your probability sample will agree to respond to your survey or participate in your study. While researchers have tried various methods (e.g., offering a monetary “token of appreciation”) to increase response rates, low response rates threaten the validity of a probability sample, especially if those who refuse are systematically different from those who eventually participate.
  2. High cost. Partly because of strategies to increase response rates through “tokens of appreciation”, the cost of implementing a high-quality survey (especially through traditional face-to-face interviews) with a probability sample have increased substantially.

Some researchers, therefore, have turned to online surveys (which are much cheaper to conduct). One recent study commissioned by the Lee Kuan Yew School of Public Policy on Singaporeans’ perception of class markers did this.


Screenshot of TODAYonline article on class perceptions. Retrieved July 16, 2019.

Figure 6.3: Screenshot of TODAYonline article on class perceptions. Retrieved July 16, 2019.


The newspaper article reports the following:

While Dr Dodgson acknowledged that the sample size was relatively low, with a 4.25 per cent margin of error, she told TODAY that the open-ended nature of the survey “gave greater nuance and accuracy” than multiple-choice questionnaires.


The study report also contains the following ‘infographic’, which confirms what the news article reported.


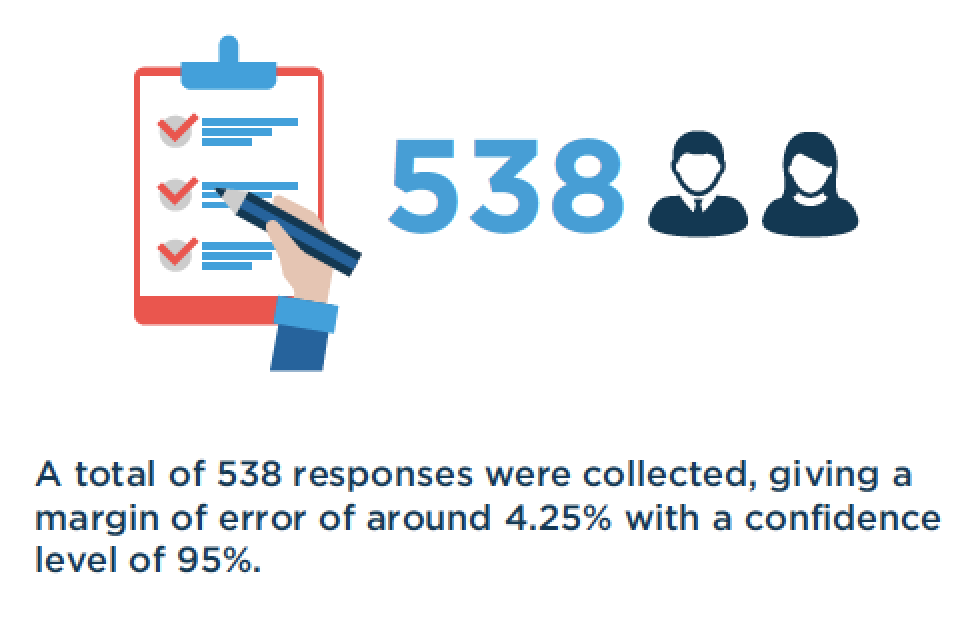
Screenshot of TODAYonline article on class perceptions. Retrieved July 16, 2019.

Figure 6.4: Screenshot of TODAYonline article on class perceptions. Retrieved July 16, 2019.


As you may recognize, this “margin of error” is something we had talked about in the previous section. I simulated the results to show the basic reasoning behind sampling theory, but you can in fact easily find online calculators purporting to calculate this “margin of error” for you44. Let’s use a random one I found. Just change the margin of error to 4.25 and the population size to ~3.5 million (Singapore resident population size) and you get back a recommended sample size of ~53045. But remember, these calculations are for a probability sample!46

Is the study in question conducted with a probability sample? The details provided are rather vague47, but my general sense is that they were not using a probability sample. The report states that:


Responses were solicited via social media and via a panel responses service. The goal with this was to attract a mixture of opinions, both from people with a pre-existing interest in the topic (whose opinions are generally weighted more heavily in political discussion, simply because they are more likely to assert them and eventually to take action on the same basis) and from those with no immediate interest (whose opinions are often discounted in political discussion, but which can have startling effects at the ballot box). Similarly, the demographics of the respondents were tracked with the aim of creating a sample that would be broadly representative of the general population.


In what seems like implicit acknowledgement that the study did not use a probability sample, some effort has been made to ensure adequate ‘representation’ through varied modes (social media and panel responses service), and through mimicking the country’s demographic composition (probably by ensuring sufficient numbers of minorities)48. It is worth noting, however, that in no way does this make it equivalent to a probability sample of all Singaporeans49. It is therefore inappropriate to calculate and use a margin of error as if it were a probability sample of all Singaporeans.

This does not mean that there is no way to use a non-probability sample to produce accurate estimates. But methods to derive estimates from non-probability samples are often context dependent (i.e., they have to be customized for each case, depending on the quantity of interest) and have different requirements beyond sample size. It requires more effort from researchers, but this is not necessarily a bad thing. Because of the practical drawbacks of probability sampling (highlighted above), statistical innovation to draw inferences from non-probability samples (often done through post-sampling adjustments) is much needed in the world of research.

‘Big data’ plays an important role here. (Matthew Salganik gives one of the best overviews on the characteristics of ‘big data’ in his book Bit by Bit, which I highly recommend). Data that is collected constantly and from many people at once allows for timely and cost-effective results, if we use the right approach to analyze them. Wang et al. (2015) (available here) use multilevel regression and poststratification (affectionately called “Mister P”) to show that accurate forecasts of the 2012 US presidential election could be obtained using data from Xbox50 users. Two points are of note here. First, the sample was large - 750,148 interviews were conducted through Xbox polls, with 345,858 unique respondents, and over 30,000 respondents completed five or more polls. Second, having strong covariates51 to adjust for non-response bias (Gelman et al. (2016), available here) and subgroup level characteristics (if more granular subgroup level estimates are of interest) are crucial to good estimation52. Neither of these was true in the study by the Lee Kuan Yew School of Public Policy discussed above. Of course, this does not mean all of the claims in that study are invalid. There are probably still insights worth learning from. However, it does tell us that we need to constantly evaluate the claims of studies against their methodology - understanding the how is often key.

References

Gelman, Andrew, Sharad Goel, Douglas Rivers, and David Rothschild. 2016. “The Mythical Swing Voter.” Quarterly Journal of Political Science 11 (1): 103–30. https://doi.org/10.1561/100.00015031.

Wang, Wei, David Rothschild, Sharad Goel, and Andrew Gelman. 2015. “Forecasting Elections with Non-Representative Polls.” International Journal of Forecasting 31 (3): 980–91. https://doi.org/10.1016/j.ijforecast.2014.06.001.

  1. Apart from having information on the entire population, through a census or administrative government data.↩︎

  2. These calculators use closed-form formulas to produce a ‘margin of error’, rather than through the more numerical/computational approach I used.↩︎

  3. The report itself does not state how they calculated the margin of error. It is my guess that this (or a variant of this calculation) is what they did. If you are aware that a different method was used, please write to me so I can correct it.↩︎

  4. More specifically, a simple random sample.↩︎

  5. For instance, how did the panel responses service recruit participants?↩︎

  6. This appears similar to quota sampling, which is a non-probability sampling method.↩︎

  7. If only it were that simple.↩︎

  8. A gaming platform↩︎

  9. Other characteristics of the sample, beyond basic demographic information.↩︎

  10. See also https://statmodeling.stat.columbia.edu/2013/10/09/mister-p-whats-its-secret-sauce/↩︎